金属加工の現場では、切削工具の寿命（Tool Life）が生産効率・コストに直結します。工具を長く使いたい一方で、加工速度も上げたい――このバランスをどう判断すべきか。そのヒントを与えてくれるのがテーラーの法則です。

本記事では、**工具寿命と切削速度の関係を数式化した経験則「テーラーの法則」**について、背景・数式・応用例をわかりやすく解説します。

テーラーの法則とは？

**アメリカの機械工学者フレデリック・W・テーラー（F.W. Taylor）**が1907年に提唱した経験則で、次のように表されます：

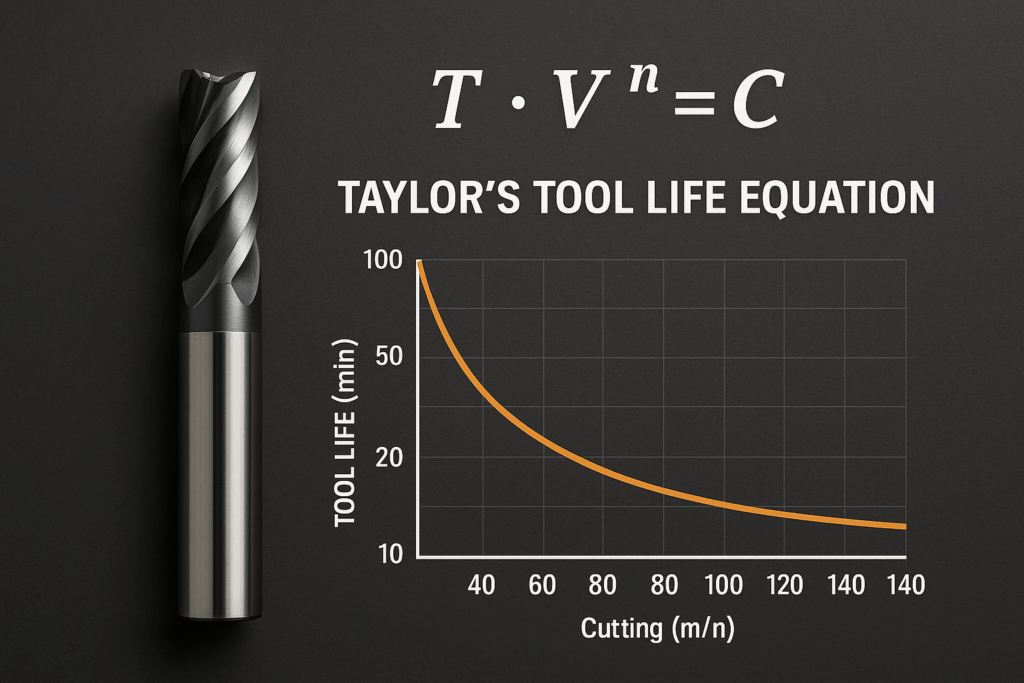
V ・T^n = C

• V：切削速度（m/min）
• T：工具寿命（分）
• n：工具材質や加工条件に依存する指数（傾き）
• C：定数（同一条件下で一定）

この式は、切削速度を上げると工具寿命が急激に短くなることを示しています。

実際の応用例

例えば、ある超硬工具で次のような実験データが得られたとします：

• V = 100 m/minで工具寿命 T = 60 min
• このとき n = 0.25 と仮定

式に代入すると、

100 ・60^0.25= C →C 〜221.7

この定数を使えば、他の切削速度における工具寿命が予測できます。

テーラーの法則から読み取れること

✅ 加工速度を上げすぎると寿命が急減する

指数 n は一般的に 0.1〜0.5 程度。つまり切削速度を2倍にすると寿命は半分以下になります。

✅ 工具選定の根拠に

異なる工具材質（超硬・ハイス・セラミックなど）で n の値が異なり、耐久性の比較指標としても利用できます。

✅ 最適な切削条件の設計に活用

生産量・工具コスト・段取り替えコストを考慮し、全体の経済性を考慮した切削条件の設定が可能です。

テーラーの法則の限界と補完

現代の加工環境では、切削条件に加え次のような要因も工具寿命に影響します：

• 切削油剤の有無
• クーラントの種類と供給方法
• 加工材の被削性（難削材など）
• 切込み量・送り速度の複合影響
• 振動やビビリなどの機械的要因

そのため、テーラーの法則はあくまで**「基礎的な目安」として活用し、実加工においては実験的データやCAE解析、IoTによる寿命管理**と併用されるのが一般的です。

まとめ：工具寿命を科学する「第一歩」

テーラーの法則は100年以上前の理論ですが、現在でも加工現場で活用される基本的な工具寿命の考え方です。

寿命と速度のトレードオフを理解し、最適な加工条件を設定することで、生産性と工具コストの最適化が可能になります。

加工の安定性とコスト削減を両立するために、まずはこの基本公式から活用してみましょう。